中学生から高校生になると、学習内容のレベルが一気に上がります。高校の授業は「一定の基礎学力がある」ことが前提で進むため、中学内容を理解しているかどうかで、理解度が大きく変わります。ここでは数学・国語・英語の主要教科について、中学での学習内容と比べてどのように発展的・応用的になるのか、さらに高校ならではの学習スタイルの変化についても具体的に見ていきましょう。

INDEX ■高校の学習内容：応用力の強化と専門知識の導入 　数学：基礎から応用へ 　国語：高度な読解力と表現力の育成 　英語：実用的なコミュニケーション能力の獲得 　新たな教科：地歴公民の分化と選択科目の多様化 ■学習スタイルの変化と進路選択への影響 　予習・復習を前提とした学習スタイルの確立 　大学受験と将来のキャリア形成への準備 ■勉強法の見直しと時間管理の重要性 ■中学と高校の教育の違いによる学び方と進路選択

　

■高校の学習内容：応用力の強化と専門知識の導入

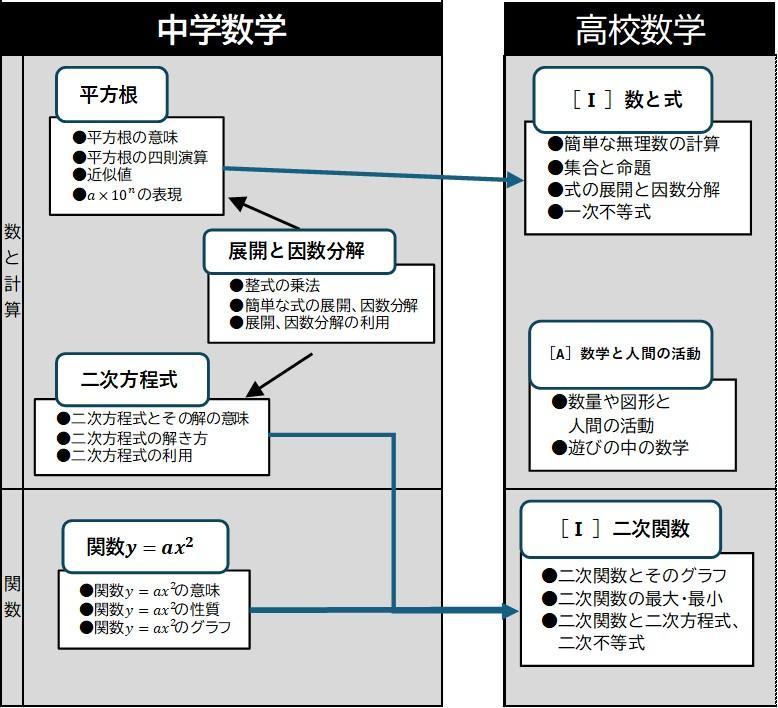
　高校の授業は、中学校で学んだ基礎を土台にして応用力を伸ばすことが中心になります。数学を例にしてみましょう。中学で学習する単元と高校で学習する単元のつながり(一部)を表したのが下の表です。高校1年生で学習する数学Ⅰ・Aでは、中学生で習ったほとんどの単元の応用・発展的内容を学習していきます。

　数学に限らず全ての教科に共通して言えることは、高校の学習内容は中学での学習の上に成り立っているものであり、その土台が不安定では授業についていくことが難しくなるということです。

　また、多くの高校では、中学で学習した基礎的な部分は当然分かっているであろうという前提で授業が進みます。そのため、中学で学習した内容は中学のうちにしっかりと理解したうえで高校に進学することが重要です。

　ここから、中学から高校への学びの違いを教科ごとに詳しく見ていきましょう。

数学：基礎から応用へ

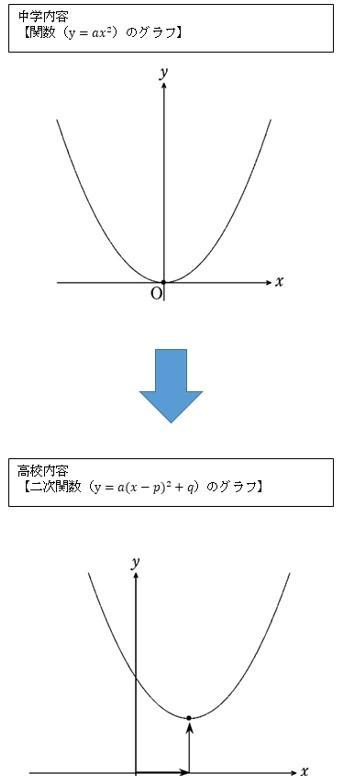
　中学数学の関数と高校数学(数学Ⅰ)の二次関数に注目して、難易度の違いを見てみましょう。下の2つのグラフを見てください。上の中学で学習したグラフでは、グラフの頂点は原点（x軸とy軸の交点）を必ず通っていました。一方、下の高校で学習する二次関数のグラフは、グラフの頂点＝原点であるとは限りません。グラフの位置も様々のため、関数の式も複雑な式となり、中学のとき以上にグラフを正確に描く力を必要とします。

国語：高度な読解力と表現力の育成

　中学国語では「小説の登場人物の気持ちを読み取る」「随筆の主題をつかむ」など、比較的わかりやすい読み取りが中心です。しかし高校に進むと「評論文」と「古典」の比重が大きくなり、中学で培った「内容を正しく理解する力」を前提に、より抽象的で論理的な読解力が問われます。

　例えば評論文では「環境問題」や「AI」といった社会的テーマから「哲学」「思想」「芸術」などの抽象度の高い本質的な問いや主張を読み解く必要があります。そのためには、段落ごとの要旨をまとめながら、解答の根拠を読み取っていく力が欠かせません。

　また、古典では中学で触れた「竹取物語」や「枕草子」が、高校では「徒然草」「平家物語」などに広がり、文法や古語の知識を用いて正確に読解することが求められます。「係り結び」や「敬語法」の理解不足が、意味を誤解する原因になりがちです。

　このように、高校の国語では「論理的に読み解く力」と「古典文法を用いた正確な解釈」という二つの力を養うことが中心となり、単なる感想ではなく「根拠をもとにした解答」がより必要とされてきます。

英語：実用的なコミュニケーション能力の獲得

　中学英語ではbe動詞や一般動詞などの基礎文法を学び、短い英文を扱うことを中心に練習しました。これを前提として高校英語では、長文読解で複雑な文構造を理解したり、英作文で意見と理由を組み立てたりしながら、英語力を養います。中学の文法や語彙を基盤にしながら、より実用的で応用的な学習へ進むのが特徴です。

　まず「長文読解」です。中学では短く、内容も比較的理解しやすい文章が中心ですが、高校では500語以上の英文を読解することも珍しくありません。テーマも科学技術や国際問題、文化比較など幅広く、単なる単語の意味を追うのではなく、段落全体の構造を把握する力が必要です。知らない単語に気を取られて全体を見失わないよう、文脈をとらえる練習が欠かせません。

　次に「英作文」です。例えば次のような問題が出題されたとします。

例題：Do you think using smartphones in class is a good idea? 50語程度で答えよ。
→解答例：I think it is not good to use smartphones in class, because students will be distracted. For example, they may play games instead of listening to the teacher.

　高校では「自分の意見を論理的な理由とともに述べる」ことが求められます。例題では「スマートフォンを教室で使うのは良い考えか」という問いに対して、賛成・反対を論理的に説明する必要があります。この力をつけるためには、日頃から「because」「for example」などを使いながら自分の考えを整理する訓練が効果的です。スピーキングについても、英作文で養った論理的に意見を組み立てる力がそのまま役立ちます。

　さらに文法面でも、中学で学んだ内容を基盤にして、助動詞＋完了形や仮定法過去などを発展的に学んでいきます。

　このように高校英語では「読む・書く・聞く・話す」の4技能を総合的に鍛え、大学受験や社会で通用する実用的な英語力を育てることが大きな目標となります。

新たな教科：地歴公民の分化と選択科目の多様化

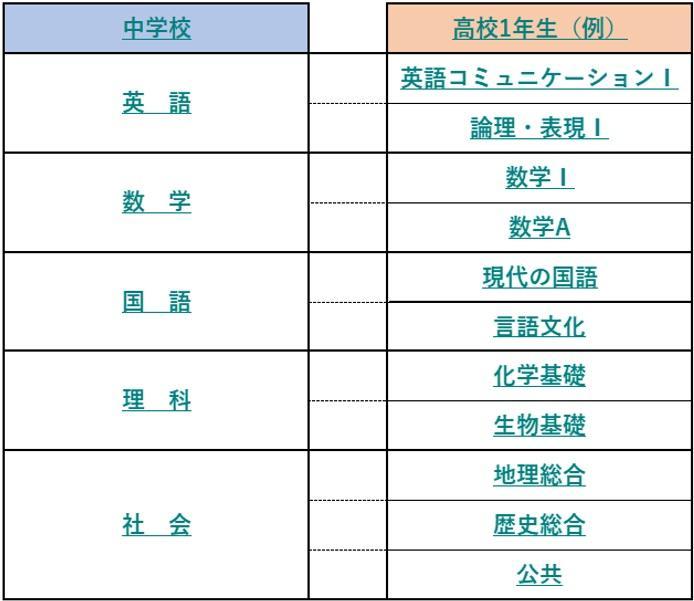
　中学では主要5教科が中心でしたが、高校に進むとそれぞれの教科がさらに細分化されます。

　英語は「英語コミュニケーション」（4技能を総合的に扱う科目）と「論理・表現」（発信力を鍛える科目）に、数学は「数学Ⅰ」と「数学A」に分かれます。理科は「物理基礎」「化学基礎」「生物基礎」「地学基礎」に、社会は「地理総合」「歴史総合」「公共」といった科目に分かれます（※社会の科目名は2022年度からの新学習指導要領における科目名称。理科・社会の学習科目は高校によって異なります）。

　このように、中学から高校へ進むと、"広く基礎を学ぶ"段階から"専門性を深める"段階へと変わり、学習量も授業数も増えていきます。

　

■学習スタイルの変化と進路選択への影響

　高校では授業の難易度も速度も増し、先生の説明をただ聞くだけでは不十分になることがあります。そのため「主体的に学ぶ姿勢」が重要です。ここでは授業スタイルの変化と、大学受験・キャリア選択につながる取り組みを見ていきます。

予習・復習を前提とした学習スタイルの確立

　高校の授業内容は難化し、速度も上がるため、一度ついていけなくなった科目は挽回が難しくなります。そのため予習・復習を欠かさないことが大切です。

予習・復習のポイント：

【英語】
・次回習う単元の文章でわからない英単語や英熟語について意味や用法を調べておく。分からなかった単語・熟語を調べたらノートにまとめておく。
・読解内容について、教科書の英文を和訳しておく。ノートの左側は教科書の内容を記入し、右側のページは和訳した日本語文を書いておくとよい。

【古文】
・教科書本文をノートに写しておき、わからない古文単語の意味を調べておく。
・古文文章の現代語訳も可能な範囲でやっておき、おおまかな内容を把握する。

【数学】
・公式の導き方や使い方をノートに整理しておき、授業で扱った例題を解き直す。
・定理や公式の証明を追い直し、根拠を理解したうえで使えるようにしておく。

　中学範囲があやふやな単元は、授業前に30分程度でいいので中学の内容を復習する時間をとると理解がスムーズになります。授業後は例題を解き直し、間違えた箇所をノートに残して復習し、定着を図ります。

大学受験と将来のキャリア形成への準備

　中学では「どの高校に進学するか」を考えることが中心でしたが、高校では「どの大学に進むか」、さらにその先に「どうなりたいか」「どういった仕事をしたいか」という将来像まで考える段階に入ります。

　希望の大学に入り、理想の未来に近づくためには、日々の積み重ねがこれまで以上に重要になります。

　高校の成績は大学受験に直結します。定期テストの結果は内申点や評定平均として反映され、多くの大学の推薦入試では重要な評価対象となります。つまり、普段の授業を大切にし、定期テストで良い点を積み重ねることが合格への基盤になるのです。

　これは受験方式の選択肢を増やすことで志望大学への合格可能性を広げるだけでなく、将来のキャリアの選択肢を広げることにも直結します。

　大学推薦入試については、別記事「大学推薦入試（総合型選抜・学校推薦型選抜）のすべてを徹底解説」で詳しく解説しています。

　

■勉強法の見直しと時間管理の重要性

　高校生になると、勉強の難度と速度が上がるだけでなく、通学や部活動に費やす時間も増えるため、学習時間の確保が難しくなります。そのため中学時代のやり方を続けるだけでは対応できず、計画的な時間管理が求められます。本記事では学習内容に焦点を当てましたが、スケジュール管理や勉強に取り組む姿勢も学力と進路選択に直結します。この点については別記事「中学生・高校生の違いを知ろう【生活習慣編】」で詳しく解説します。

　

■中学と高校の教育の違いによる学び方と進路選択

　中学から高校への進学は、学ぶ内容の深さも、将来を考える視点も大きく広がる節目です。

　高校での学びは決して特別な人だけのものではなく、今の勉強を少しずつ積み重ねていけば誰でもしっかりと対応できます。中学生のうちから「高校ではどんな学びが待っているのか」を知っておくことで、安心して一歩先のステージに進むことができるのです。

　フリーステップでは、個別指導だけにとどまらす、駿台Diverseを組み合わせたハイブリッド指導を行っています。また、デジタルLapテストやLapマスター（解説動画）などの予習・復習のサポートは、家庭でも取り組むことができ、学習場所を問いません。これらをMy Step Logというオリジナルシステムでつなぐことで、定期テスト対策と大学受験対策の両立を可能にしています。高校の勉強に対して不安に思うことがあれば、最寄りの個別指導学院フリーステップへいつでも相談にお越しください。

＜文／開成教育グループ　個別指導統括本部　教育技術研究所＞