こんにちは。藤山です。教育に関するお話をしていきます。
今回は、計算問題についてお送りします。

今回は教科教育のうち、算数・数学教育に関するお話です。教育の目的や発達心理学といった大きな話題だけが教育学ではありません。個々の教科教育に関しても、教師の個人的な工夫や生徒の自然な成長に委ねられているわけではなく、教授方法やそのために必要な意味が考えられています。「計算もできないのに応用問題なんてできないよ。」「もぉー。計算問題くらいは正解しなさい。」などと、算数・数学の基礎的な力として語られる「計算」ですが、教育学の世界ではその部分を深く考えている人もいるのです。

加法（足し算）について

まず、加法（足し算）について紹介してみましょう。

「加法が適用される場面は、合併・増大・求大と呼ばれるような場面を想定することができる。」（崎谷2000）・・・・。例によって学問で使われるわかりにくい表現ですので、説明します。

「合併」とは、二つのグループの数を合わせて一つのグループにした時の個数を求めるなど、まとめていくつになるのかを考えるときに使う、という意味です。太郎君が飴玉を3個持っていて、花子さんは飴玉を7個もっています。合わせるといくつでしょう。という時足し算を使います。当然です。

「増大」とは、一つのグループに何かが付け加わった結果を求める考え方です。太郎君が7個のボールを持っています。さらに3つもらいました。いくつでしょう。という考え方です。個数の場合では「合併」とあまりとらえ方が変わりませんが、3時17分の3分後は？というように、時刻と時間の違いなど二つの数が同質なグループと考えられないときは、この考え方になります。

「求大」とは、二つの集合があって、その差から、大きいほうの数値を求める、といった考え方です。太郎君はカメを3匹飼っています。花子さんはそれよりも4匹多く飼っているそうです。さて花子さんは何匹のカメを飼っているのでしょうか。という時に使う足し算がこれに当たります。

自然数（個数や順序などを表す正の整数）の場合はさておき、負の数が出てきたときでは、答えが大きくなるわけではないので「求大」の概念に違和感がありますが、ともかく「太郎君は3万円の貯金があって、花子さんは－1万円の貯金（1万円の借金）があります。合わせるとどうなるでしょう。」という問題を考えますと、「マイナスの貯金＝借金」のように反対語による言い換えで、何とか意味は通じ、マイナスの足し算の説明も「合併」でいけそうです。

このように減法（引き算）などほかの計算に関しても説明のための概念が議論され指導に応用されています。

計算と式

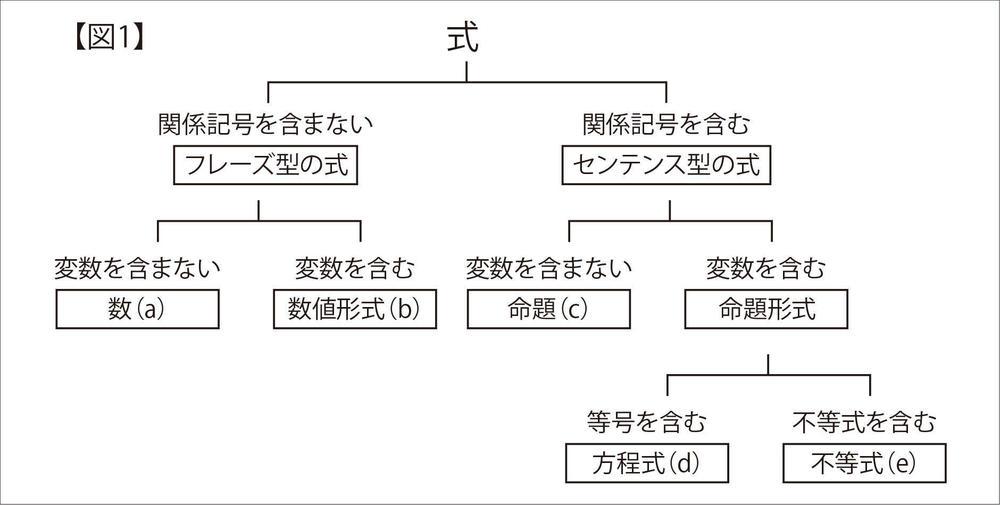
さて、計算には計算式が存在します。その「式」についても踏み込んで考えられていました。まず、図のように式を分類してみましょう。

■図1

まず、「関係記号を含まない（フレーズ型）」と「関係記号を含む（センテンス型）」の違いは、7＋3がフレーズ型7＋3＝10というのがセンテンス型、という意味です。日本語に置き換えると、「7に3を加える」がフレーズ（＝単語の集まり）、「7に3を加えると10と等しいです。」というのがセンテンス（＝「思考や感情を言葉で表現する際の完結した内容を表す最小の単位」（大辞林））という意味での分類です。

【図1】について順に例を書いてみると、（a）3×5、（b）x×5（＝5x）、（c）3×5＝15、（d）x×5＝15、（e）x×5　10という事になります。ところで、世界の学校ではこれと同じ記号を使った式が使われています。実は数学の世界には、国境も宗教による違いもありません。音楽で使う楽譜と同じように万国共通です。（数の概念のない少数民族がいるという話もありますが、国の教育レベルで考えると世界共通語だといえます。）そのおかげで、海外経験のない人が外国の大学などを受験するときには、数学が一番ストレスを感じず、むしろ久しぶりに言葉が通じる人に出会ったような喜びすら感じるといいます。

計算と道具

ところで計算を意味する（calculation）という英単語の語源は、ラテン語のcalculusで、計算用の小石を表す言葉です。（因みに医学用語で「結石」や「歯石」のこともcalculusと呼ぶそうです。）漢字の「算」も数を数えること、またはその道具を表す言葉だとされています。つまり、古来は何らかの道具を使って計算をしていたようです。小さい子どもが指を折って数えますが、その延長がこの小石や算木・算盤（さんばん）といった道具だったのでしょう。中国伝来の「そろばん」（漢字では「算盤」と書きますが（さんばん）と区別するためにひらがなで表記します。）はその道具の進化系だといえるでしょう。

そろばんは、それを使って計算できるだけでなく、それをイメージすることで暗算を行うことができるところに価値があります。実際そこまでのスキルが身についていると、電卓よりも早く計算することができます。しかし、数年前まで小学校では電卓も使わせており、そろばんの指導時間は5～6時間程度しかなく、結局どっちつかずになっていた印象があります。（改訂された指導要領では電卓の使用を取りやめたわけではありませんが、指導要領改訂のポイントに「筆算による計算の指導をしたうえで、」との但し書きがありますので、多くの学校では結局電卓は使われなくなったようです。）

ちょっと脱線しますが、同じ計算の道具である「計算尺」はご存知でしょうか。ジブリ映画「風立ちぬ」で主人公の堀越二郎が飛行機の設計に使うシーンでも登場していました。当時では物理系技術者の必需品であり、月面着陸に成功したアポロ計画でも軌道計算の確認用やコンピューターの故障に備えて司令船に搭載されていたというこの道具、今では関数電卓やコンピューター、ついにはスマホのアプリにすら押されてほぼ絶滅してしまいました。

■計算尺

中学校や高校の数学でその使い方の授業を受けたのは今50歳後半以上の方だと思います。ほんの8年前までは無線技士の国家試験では持ち込みが許可されていましたが、そんな制度すら無くなった今日では、この型は生産されなくなり、入手することすら困難になってしまいました。（実は今日では円形のものは手に入ります。少し使いにくいのですが乗除や平方根、立方根はもちろんの事、三角関数や対数の計算が有効数字3ケタの精度でできるのです。もちろん電池を使わずに。）

筆算と暗算

閑話休題、人はいつごろから暗算していたのでしょうか。これだけは形が残らないものなので永遠の謎かと思いきや、紀元前14世紀の古代エジプトの文書に「暗算をするときにはおしゃべりをするな」という記述があるそうですし、古代ギリシャの哲学者アリストテレスも暗算の重要性を説き、同じく古代ギリシャの遺跡から九九の表が出土されていることから、むしろ紙のない時代は暗算のほうが実用的だったようです。それが証拠に、逆に筆算が歴史上に登場するのはなんとそれから1500年も後の13世紀になっての事です。位取りを原理とするインドの記数法をイタリアの数学者であるフィボナッチがヨーロッパに伝えたところから始まったといわれていますが、紙の生産量の増大を背景に、一気にヨーロッパで広まっていったのでした。

日本で「暗算」や「筆算」という言葉が使われ始めるのは明治5年（1872年）の「小学教則」が初めてのようです。その中には「筆算ト暗算トヲ隔日練習セシム・・・（原文では暗算の暗は「諳」という漢字を使っています。）」とあるように日々交互に練習することが推奨されていました。

平成元年の学習指導要領でも「暗算を筆算や見積もりに生かすように配慮するものとする。」とありますので、そのあと小学校で導入された電卓を使う授業でも、電卓を使う前におよその答えを暗算で見積もるといった指導が期待されていたことになります。

このように計算問題一つをとっても、その意味や歴史、指導方法を考えていくのが教育学です。早く答えを出すためにドリルのようなもので数多く反復練習して、という事も大切ですが、今一つ立ち止まって、その意味や背景を考えてみると、算数や数学嫌いの人でも、違った見方ができるかもしれません。

【参考文献】

・大辞林　第3版　三省堂　2006

・岩崎秀樹　「暗算」「筆算」　算数・数学科　重要用語300の基礎知識　明治図書2000

・岩崎秀樹　「式」算数・数学科　重要用語300の基礎知識　明治図書2000

・日本教育工学事典　日本教育工学会編　2000

・崎谷眞也　「加法の意味」　算数・数学科　重要用語300の基礎知識　明治図書2000

・小学教則（抄）　明治5年9月8日　文部省布達番外　1872

＜文／開成教育グループ　入試情報室　藤山正彦＞

【フリステWalker 第137号（2020.3月）掲載】