中学生の学習において、まず目指してほしいのが定期テストの点数アップです。今回は定期テストに対応する力を養うための、数学の効果的な勉強方法について紹介します。

■数学の基礎力を身につける方法

　まずは、数学の基礎を固めていきましょう。ここでの数学における基礎力とは、「公式が使用でき、教科書の例題を正しく解ける、計算できる力」のことを指しています。基礎力を伸ばすことで解ける問題が増え、学習のモチベーション向上にも繋がります。ここでは、数学の基礎力をつけるためのポイントをいくつか紹介していきます。

教科書の例題で基礎を固める

　数学の基礎を固めるため、教科書の例題に取り組む方法について、ここでは、中2で学習する一次関数を例に取り上げます。それぞれのゴールを意識しながら、例題に取り組んでみましょう。

例題：「y=2x+5、x=3 のときの y の値を求めなさい。」

ステップ1：問題の意味をつかむ
　まずは「求めるもの」を明確にしましょう。
「xに3を入れたときのyの値を出す問題だな」と自分の言葉で整理します。

ステップ2：例題の解説を読む
　次に、正しい手順を把握し理解します。
「x = 3 を代入する」と書かれていれば、なぜそうするかを理解し、式 y=2x+5に 3 を入れて y=2×3+5=11 となることを確認します。

ステップ3：自力で解く
　ステップ2を、解法を見ずに再現できるようにします。正答することも大切ですが、先ほど練習した正しい手順で解くということに重きを置いてください。

ステップ4：類題に挑戦
　最後に類題に挑戦しましょう。例題の続きに載っている練習問題や、教科書傍用問題集を使用して、ここまでの理解したことを別の問題でも使えるか確認していきましょう。

この4ステップで、例題が「わかった気がする」から「自分で解ける」に変わります。

公式をしっかり覚えるコツ

　中学生が公式をしっかり覚えるためには、ただ暗記するのではなく、工夫して取り組むことが大切です。まず、公式の意味や成り立ちを理解することで、記憶が深くなり応用にも強くなります。そして、実際の問題に何度も取り組んで繰り返し使うことで、自然と公式が頭に定着していきます。

　例えば、中3で学ぶ因数分解の公式「x²+(a+b)x+ab=(x+a)(x+b)」は、次の2ステップで覚えると効果的です。

ステップ1：公式の意味を理解

　ここでは、式変形の前と後で、何がどう変化しているのかきちんと目で追って、説明できるようになることが目標です。

　そのためには「x²+(a+b)x+ab → (x+a)(x+b)」となることだけではなく、「(x+a)(x+b) →x²+(a+b)x+ab 」と展開して元に戻ることを確認しておくことが重要です。この因数分解の公式には「→」ではなく「＝」が使われていることをきちんと理解してきましょう。

ステップ2：反復練習

　次に、実際に問題を解いてみます。「x²+5x+6=(x+2)(x+3)」など、よく出る形にたくさんふれましょう。「足して5、かけて6になるのは2と3」など、数の組み合わせに慣れていけば、自然とよく出るパターンが身につき、計算スピードと正確性のどちらも向上が見込めます。

　このように、理解と反復を組み合わせることが、公式を確実に身につけるためのポイントです。

基本問題での計算力向上

　計算力をのばすには、難しい問題に挑戦することより、むしろ基本問題にくり返し取り組むことが大切です。これにも教科書の例題や練習問題がおすすめです。基本問題をくり返すことで、はじめは丁寧でゆっくりな計算であっても、丁寧なまま反射的に解法を思いつき、自然と手が動き、問題を解くことができるようになるでしょう。

　ここで、もし間違えた場合は、その問題はノートにまとめて、「なぜ間違えたのか」を見直すことで、同じミスを防げます。また、問題に取り組む時には時間を計るようにすると、集中力と処理力がアップします。ふり返り・時間意識の2つを意識しながら取り組めば、確かな計算力が身についていきます。

■数学の理解を深めるためのステップ

　数学の基礎を固めたら、次は数学の理解を深め、力を伸ばしていきましょう。ここでは、いくつかポイントを述べていきます。

間違えた問題の見直し方

　過去記事「中学生のための定期テスト勉強法ガイド」の「数学　理解を深めるテクニック」を参照下さい。

ノートの効率的な使い方

　過去記事「中学生のための定期テスト勉強法ガイド」の「ノートの取り方と復習のコツ」を参照下さい。

問題文を論理的に読み解く力を養う

　数学の問題文を論理的に読み解くためには、次の手順①～⑤に沿って考え、解答を作成していくことが大切です。まず、問題文から情報を整理し、「何が分かっていて、何が分かっていないのか」を意識することが出発点です。

①何を求めるのか

②求めるための条件は何か

③与えられている条件は何か（②に使えるか）

④ ②－③をしてあとどの条件を導く必要があるか

⑤解答を始める

　これらの手順で情報を整理して読み解き、解答へと進んでいきます。

　例えば、道のりを求める方程式の文章題を解くには、次のステップで考えていきます。

例題：家から図書館に行くのに、自転車を使って毎分250mの速さで行くと、毎分60mの速さで歩いて行くより38分早く着くという。家から図書館までの道のりを求めなさい。

ステップ1：【何を求めるのか】この文章題では、家から図書館までの距離を求めることがゴールとなっています。
ステップ2：【求めるための条件は何か】「距離=速さ×時間」で求められます。速さはすでに問題文の中で述べられているので、時間に着目して解答を考えていく必要がありそうです。発展的な内容になるほど、求めるための条件が導きにくくなっていきます。その場合はステップ2を飛ばして、他に有用な情報・条件は無いか考えていきます。

ステップ3：【与えられている条件は何か】与えられている条件は、「自転車を使って毎分250mの速さで行く」場合と、「毎分60mの速さで歩いて行く」場合があり、自転車と徒歩では、かかる時間に38分の差があるということです。

家から図書館までの距離をxmとすると、家から図書館までかかる時間は、

自転車の場合は x/250分

歩く場合は x/60分　となります。

自転車で行くほうが歩くより38分早く着くため、家から図書館までかかる時間に着目すると、以下の方程式を立てられます。

x/250+38=x/60

ステップ4：【残りはどの条件を導く必要があるか】与えられている条件だけでは答えが求められない場合、さらに必要な条件を考えていきます。この例題の場合、ステップ3で立てた方程式を解くとの値が出てきそうです。そのため、追加で導くべき条件はありません。

ステップ5：【解答を始める】ステップ3で立てた方程式を解くとx=3000の値が出てきます。家から図書館までの道のりは3000mがこの例題の答えとなります。

　このように、手順立てて文章題を考えていく練習を重ねることで、数学の問題に対して落ち着いて論理的に向き合える力が身についていきます。

■応用力を伸ばすための取り組み

　数学の応用力がついてくると、難しい問題にも対応することができるようになります。ここでは応用力を鍛える方法をいくつか紹介していきます。応用力の確認には、模擬試験を活用し、実践練習を積んでいきましょう。

応用問題への挑戦と段階的な練習

　数学の応用問題に挑戦するためには、段階的に練習を積んでいきましょう。まず、公式を覚えたり、基本問題を繰り返し解いたりして、基礎をしっかり身につけることが重要です。これにより、難しい問題でも「使える知識」が自然と備わります。また、「○問題文を論理的に読み解く力を養う」で説明した5つの手順（①何を求めるのか　②求めるための条件は何か　③与えられている条件は何か（②に使えるか）④ ②－③をしてあとどの条件を導く必要があるか　⑤解答を始める）で問題を考えていく練習をしていくと、問題文がパターン化して見えてきます。

・今の条件で導けるのは何か

・どの条件がそろえば、何が導けるのか

　このあたりが見えてくると、定期テストの標準レベルまでは、問題を一読すれば、今の条件で導けるのは●●で、次に▲▲が出て・・・と解法が導けるようになります。応用レベルの問題でも踏むべき手順は同じです。基礎力を確実に固め、演習を積み重ねていくことで、数学の解法を導き出す力がついてきます。

図やグラフを活用した問題の解き方

　数学の図やグラフを使った問題を解くには、情報を正しく読み取り、意味づけをしながら考える力が必要です。まず、図やグラフに自分で数値や線を加えて書き込みながら整理することで、問題の構造がより明確になります。次に、それぞれの図やグラフが何を表しているのかを言葉で説明する練習をすることで、内容への理解が深まります。また、問題文や導き出した答えと図・グラフを何度も見比べることで、条件の読み違いや見落としを防ぎ、確実に解答にたどり着くことができます。一次関数の例題を用いて、各ステップを説明していきます。

例題：下の図の直線の式を求めなさい。

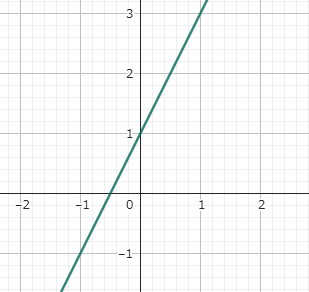
ステップ1：図に書き込む
　たとえば、x＝0のときy＝1なので、点(0, 1)をグラフに書き入れて確認します。

ステップ2：言葉で説明する
　「xが1増えるとyは2増える」というように、変化の意味を言葉で整理します。

　整理した情報から、グラフの式は、y=2x+1と分かります。

ステップ3：文と図を見比べる
　グラフがy=2x+1だとすると、グラフは点(-1,-1)を通るはずです。計算結果と一致するかグラフを確認します。

　こうした丁寧な確認と作業の積み重ねが、図やグラフを使った問題への対応力を高める鍵になります。

■定期テストのための対策

　続いて、内申点に直結する定期テストの対策を紹介していきます。過去記事の「中学生のための定期テスト勉強法ガイド【定期テスト攻略の基本】」も参照ください。

効率的な学習スケジュールとテスト対策

　定期テストを攻略するには、定期テストをゴールとして逆算し、「いつまで何を学習するか」を決めることから始めます。定期テストは年間で4～5回ありますので、各テストでおおよそのテスト範囲を予測しておき、いつまでに「問題集を完成させる」や「●●の単元を復習する」という短期目標と立てていき、スケジュールを作成します。

　また、テスト自体がどのように作問されているか、も重要です。例えば出題範囲の構成比率が、ノートや授業内容から4割、問題集から4割、応用問題2割などです。

　とはいえ、まだ学習していない単元がどこまで進められるかを判断することは、容易ではありませんし、その上でスケジュールを組むことは、どの単元が重要（テスト頻出）かを判断する必要があります。ましてや、各テストがどのように作問されているかを自身で見比べて判断することは並大抵の理解度では難しいでしょう。

　フリーステップでは、これまでの全生徒の学習ログから各学校の定期テスト範囲を割り出すことが可能なS－CUBEというツールがあります。また、My Step Log（マイ ステップ ログ）という機能では、一つ一つの授業の理解度や進捗管理から、各教科の要対策（苦手）単元や、定期テストの予想点数、これまでの成績推移にいたるまで、管理することができます。また、教室チーフが学習プランナーとして、生徒それぞれの進捗状況や単元理解度を定期的に確認し、必要に応じて学習計画を調整します。

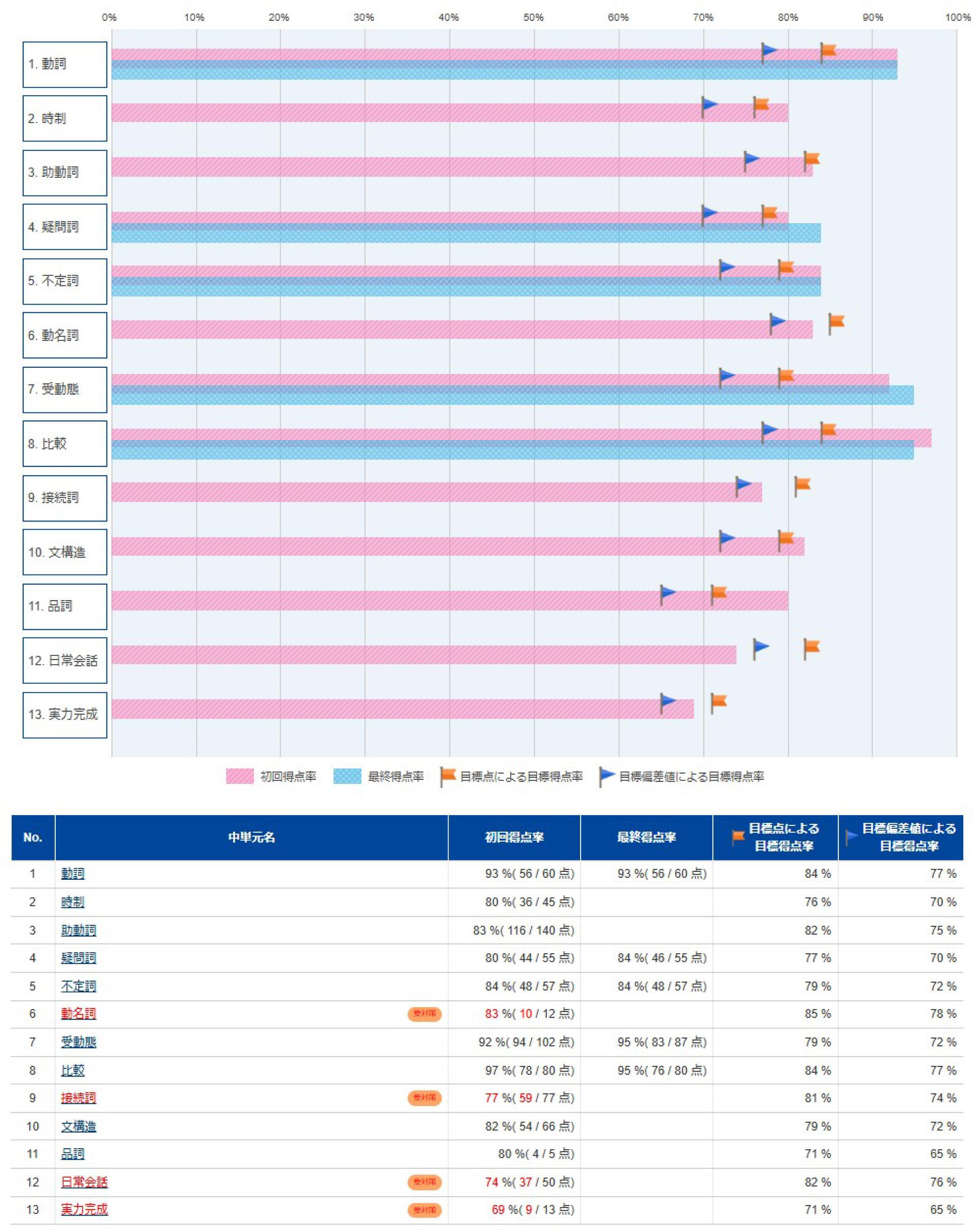
※画像は英語のカリキュラムです。

　ここからは、フリーステップで行う効果的なテスト対策を、《テスト2週間前まで》と《2週間前からテスト本番まで》に分けて説明していきます。

効果的な定期テスト対策の進め方～2週間前まで～

　毎年中学生だけで約8,000人以上にお通いいただいているフリーステップでは、前述したように、My Step Logに全生徒の学習ログが蓄積されています。これを用いて、各教室チーフが学習プランナーとしてテスト範囲を予測し、テストまでの日程から生徒の目標点や理解度に合わせたカリキュラムを作成します。また各授業の終わりには、全国の定期テストを分析して作問されている、「Lapテスト」という確認テストを行い、理解度チェックを行います。これにより、各授業・単元のどこを苦手としているのか、つまり、どの単元の復習を優先すべきかをデータとして蓄積していくことができます。

　どの定期テストも範囲は広いでしょうし、多くの中学校では、テストの直前まで授業が進むことでしょう。当然ながら、テスト範囲の授業が終わってから、「どこを復習しようか」と考えだすと間に合わなくなります。しかし、フリーステップにはMy Step Logがあるので、これらの問題を全て解消できるというわけです。さらにこの復習以外に、フリーステップでは、先を見据えたカリキュラム作成と進捗管理も行います。テストの2週間前にはテスト範囲の学習を終わらせ、テストの予想問題や、より実践的な問題に取り組める状態にするためです。これで、生徒は余裕を持って、テスト2週間前を迎えられます。

効果的な定期テスト対策の進め方～2週間前からテスト本番まで～

　いよいよテストが近づいてきました。とはいえ、まだテスト範囲は出ていないでしょう。「テスト範囲が出るのを待ってからテスト勉強を追い込むぞ！」とどれだけ意気込んでいても、テストまでに十分な対策ができない方が大半でしょう。

　フリーステップにはMy Step Logがあるので、テスト範囲が出ていなくても予測できていますし、復習しておくべき苦手単元も、生徒それぞれに対して割り出されています。テスト2週間前からは、それぞれの苦手単元の復習を進めましょう。そして、テスト1週間前になれば、いよいよテスト範囲が出ることでしょう。フリーステップの塾生であれば、ここでテスト範囲の膨大さや出題単元の難しさに焦ることはありません。むしろ、さらに磨きをかけるため、テストの予想問題に挑戦していきます。フリーステップは、通常授業用でもそうですが、テスト直前対策にもオリジナルの専用教材を用意しています。このように、テストという目標から逆算してスケジュールを組み、カリキュラム通りに勉強することで、効果的なテスト対策を進めることができます。

■まとめ 計画的かつ継続的に数学力を伸ばそう

　中学生が数学を効果的に学ぶには、定期テストを見据えた計画的かつ継続的な学習が重要です。中学1・2年生は定期テスト対策を軸に基礎固めや積極的な演習を積んでいき、さらに中学3年生はその先の高校受験も見据えて、学習内容の総復習に取り組んでいきましょう。

　まずは教科書の例題にしっかり取り組み、公式の意味を理解しながら繰り返し使うことで、基礎力を身につけます。基礎的な計算練習を積み重ね、ミスの振り返りや時間を意識した学習を行うことで、計算力の向上も図れます。さらに、問題文に対して、手順を踏んで考えていく練習をしていくことで、論理的に解法を導き出す力も伸びていきます。応用力を高めるための方法も、基本は変わりません。基礎力を固め、手順に沿って解法を考えていく演習を重ねましょう。定期テスト対策としては、学習計画を逆算して立て、苦手単元の把握と復習を行い、予想問題にも挑戦していきましょう。

　このように基礎から応用へと計画的にステップを踏み、定期テストの点数を確実に上げていくことで、数学の理解と得点力の両方をバランスよく伸ばすことができます。

＜文／開成教育グループ　個別指導統括本部　教育技術研究所＞