高校数学は中学の数学とは異なり単に「公式暗記の科目」ではありません。実際には理解を積み重ね、演習を繰り返すことが成績向上の鍵です。しかし、途中でつまずくと苦手意識がどんどん強まり、その後の内容が頭に入らなくなることも少なくありません。

　数学は大学受験において英語、国語と並ぶ重要科目です。特に理系の受験生にとっては最重要な科目となります。ここでは、そんな数学の効果的な勉強法や苦手克服のための具体的なステップを紹介します。今まさに数学に頭を悩ませている人は参考にして、苦手意識を克服しましょう！

INDEX ■高校数学が難しいと感じる理由 ■高校数学の範囲を知ろう：数学ⅠA・ⅡBC・Ⅲの特徴 ■苦手分野を見極める方法 ■教科書・資料集でのインプット方法 ■効果倍増の復習法とスケジュール管理 ■ケアレスミスへの心構えと改善策 ■まとめ：高校数学は基礎と反復が最大のポイント

　

■高校数学が難しいと感じる理由

　具体的な勉強法を紹介する前に、高校数学はどうして難しいと感じてしまうのでしょうか？苦手な人が多いということは、それ相応の理由があるはずです。

①中学数学からのギャップと抽象度の高さ

　中学数学と高校数学は全くの別物と言われるほどに、両者には学び方や内容の性質に大きな違いがあります。中学数学では主に計算力を中心に学習しますが、高校数学では「なぜ、そうなるのか」を論理的に考える思考力が問われます。この違いは高校入試と大学入試の問題をみると一目瞭然です。高校入試では基本的な計算等を問われるのに対して、大学入試では答えにたどり着くために定義や条件を正確に扱い、筋道を立てて説明する厳密さが問われています。

　さらに、このギャップを広げているのが抽象度の違いです。中学数学では方程式の解き方や図形の性質など実生活に結びつくような概念を中心に学習する一方、高校数学では関数、数列、ベクトルなどといった抽象的な概念を学ぶため、イメージがつかみにくくなります。

②積み上げ式の理解不足が招くつまずき

　高校数学は学習する範囲も中学数学とは比べ物になりません。さらに、学習内容は積み上げ式となっており、ひとつの単元で学んだ知識や考え方は他の単元につながり、さらにその先の応用問題と発展していきます。つまり、途中で「わからない」を生み出すと、そこからドミノ倒しのように、その先の単元もわからないことが増えていき、苦手意識が大きくなってしまうのです。さらに高校の授業では範囲の膨大さゆえ、スピードも早く、理解不足があれば、置いてけぼりにされてしまいます。逆に言えば、基礎を1つひとつ積み重ねることで、次の内容もスムーズに理解することができるというわけです。

　

■高校数学の範囲を知ろう：数学ⅠA・ⅡBC・Ⅲの特徴

　では、実際に高校数学ではどのようなことを学ぶのでしょうか？ここでは「数学IA」「数学IIBC」「数学III」に分けて学習する内容を詳しく紹介します。

数学ⅠA：二次関数・図形と計量などの基礎

　数学IAでは以下の内容を学習します。

＜数学I＞

【数と式】
　数の種類（整数、実数、虚数など）や集合といった基本的な概念を学習した後に、式の分野では中学数学でも学習した式の展開や因数分解の発展内容を学習します。さらに、新しく不等式の解き方についても学習します。

【図形と計量】
　新しい概念として「sin」「cos」「tan」を学習します。また、それらの三角比に対する様々な性質についても学習します。新しい概念を学ぶため、ここでつまずく高校生も多いです。

【二次関数】
　中学数学で学習した二次関数を一般的なもので考えます。具体的には、頂点が原点上でない場合や、上に凸な場合などです。また、二次関数に関する最大・最小、二次方程式とのつながりについても学習します。

【データの分析】
　データに対する、平均・分散・標準偏差、中央値、最頻値などの基本的な概念を学習します。

　また、箱ひげ図や散布図などの図の読み取りについても学習します。

＜数学A＞

【場合の数と確率】
　中学数学での簡単な確率とは異なり、複雑な確率についても考えます。場合の数として順列や組合せといった概念を学び、その後、確率について詳しく学習します。

【数学と人間の活動（旧課程：整数の性質）】
　基本的には旧課程と同様、約数や倍数、不定方程式などの整数に関する様々な性質について学習します。

【図形の性質】
　主には三角形、円の性質について学習します。具体的には、三角形の外心や内心、チェバの定理・メネラウスの定理、方べきの定理などです。

　数学IAで学習する内容は基本的な部分でもあるため、難易度が高いことは学習しません。しかし、ここで学習する内容は以下の数学IIBCや数学IIIにもつながる基本的な分野であるため、理解不足があると今後の内容理解に影響を及ぼす可能性があります。

数学ⅡBC：三角関数・数列・ベクトルへの応用

　数学IIBCでは以下の内容を学習します。

＜数学II＞

【いろいろな式】
　数学Iで学習した因数分解をもとに、三次式の展開や因数分解、二項定理などを学習します。また、正式についての割り算や、恒等式、等式・不等式の証明なども学習します。その後、新しい概念として「複素数」を学習します。また、方程式に関する様々な定理、具体的には解と係数の関係、因数定理などを学習します。

【図形と方程式】
　これまで学習してきたグラフを座標平面上で考えます。分点や点と直線の距離などを数式を用いて表現します。また、円の方程式について学習して、円に対する接線や直線との関係を学習します。さらに、軌跡や不等式の表す領域についても学習します。

【三角関数】
　数学I【図形と計量】で学んだ三角比をさらに拡張したものを学習します。具体的には、三角関数における加法定理や2倍角の公式、和積・積和の公式、三角関数の合成について学習します。

【指数関数・対数関数】
　新しい概念として「対数」を学習します。また、指数と対数の関係や、方程式、不等式、グラフについても学習します。

【微分法・積分法】
　新しい概念として「極限」「微分」「積分」を学習します。微分法では、その定義や微分を用いたグラフの描画を学習します。さらに、三次関数や四次関数についても学習します。積分法では、その考え方や積分を用いた面積の求め方について学習します。

＜数学B＞

【数列】
　新しい概念として「数列」を学習します。数列のいくつかのパターンとして、等差型・等比型・階差型を学習します。また、数列の応用として、群数列や漸化式についても学習します。さらに、証明の新しい手法として数学的帰納法についても学習します。

【統計的な推測】
　数学Aで学んだ確率の応用として、確率を変数とする確率変数やそれによる分散、標準偏差、期待値を学習します。また、試行回数と確率の関係として二項分布を学習します。さらに、連続的な確率変数に対する、確率密度関数や正規分布などについても学習をします。また、統計的な推測として母集団の推定や検定について学習します。

＜数学C＞

【ベクトル】
　新しい概念として「ベクトル」について学習します。ベクトルに関する、基本的な考え方である　成分や大きさ、内積などについて学習し、その後ベクトルを用いたベクトル方程式や平面、空間ベクトルについて学習します。ベクトルはこれまでと異なることを考えるため、理解不足になりやすい分野です。

【平面上の曲線と複素数平面】
　数学IIで学んだ複素数を座標平面上で考えます。複素数平面上での和・積等を学習した後、極形式について学習します。さらに極形式を用いて、複素数の積や商を考え、ド・モアブルの定理などを学習します。また、平面上の曲線として、円以外に楕円や双曲線についても学習します。

　数学IIBCは数学IAよりも専門性が高く、難易度差を感じる高校生が多いです。さらに、これらの内容は数学IIIにも直結する内容となっています。また、文系の学生であったとしても国公立志望であればここまでの内容が共通テストで必要となります。

数学Ⅲ：微分積分でもっと広がる総合力

　数学IIIでは以下の内容を学習します。

【極限】
　数学IIでの極限をさらに専門的に学習します。数列の極限について考えた後、関数についての極限を考えます。また、この分野で新たに無限大の考え方についても学習します。

【微分法】
　数学IIでの微分法より高度なものを学習します。具体的には、無理関数・分数関数、三角関数、対数関数の微分を学習します。それらを用いて関数の変曲点、複雑な関数のグラフの描画なども学習します。

【積分法】
微分法と同様、数学IIよりも高度なものを学習します。合成関数や、置換積分、部分積分の考え方を学習し、三角関数や対数関数などの積分についても学習します。その後、応用として面積や体積についても学習します。

　数学IIIについては基本的には数学IIにおける極限、微分・積分法の拡張となります。そのため、数学IIでの基本知識が欠けていると一気につまずいてしまいます。また、理系の学生は大学受験において必須の科目となるので数学IIIの完成度が志望大学の合否に直結するといっても過言ではありません。

　

■苦手分野を見極める方法

　積み上げ式の理解不足の点でも書いたように、一つの苦手は他の分野にも影響を及ぼすのです。つまり、苦手分野の克服は成績アップの秘訣です！ここでは、その苦手分野を発見する方法を紹介します。

テスト結果や模試を活用する

　みなさんはテストや模試が返却されたら、点数だけ見て満足していませんか？テストや模試こそ苦手発見の一番重要なデータです！端的に言えば、間違った分野＝理解が完璧でない分野ということです。　　

　具体的なチェック方法になりますが、定期テストであれば出題範囲は限定されているので、すぐにどの分野が苦手かは確認できます。多くの高校では普段使うワークの問題から出題されているので、より詳細に苦手な内容を確認できます。模試であれば、解答解説に丁寧に出題分野が書かれているので、自分の答案の正答率と照らし合わせて苦手分野を洗い出すことができます。

理解できていない要点を洗い出すチェックリスト

　普段の学習の中で、チェックリストなどを設けると理解できていない分野が可視化され簡単に見極めることができます。例えば、問題集を解く際に星の数で評価する方法があります。具体的には

★★★＝模範解答と同じ、または似たような解答でかつ正解している。　

★★＝若干のニュアンスや解答に不自然な部分がみられるが、正解はしている。　

★＝解答の道筋は正しいが、不正解や公式ミスがある。　

(★なし）＝見当違いな解答をしている。

などです。この他にもチェック方法はありますが、筆者は現役時代、これで各問題の評価をしていました。そして、全分野実施後に★の数が少ない分野＝苦手分野となり、かつ★の少ない問題から優先して復習をすれば、効率的に苦手なものを復習することができます。

基礎固めから始める！効果的な勉強手順

　ここまででもよくわかる通り、高校数学では基礎からの積み重ねが命です。ここでは効果的な勉強法をいくつか紹介します。

　

■教科書・資料集でのインプット方法

　インプットで一番効果的なのは教科書・資料集を用いた学習です。問題を解くことができることも大切ではありますが、基本的な公式の意味を理解することが前提にあります。公式や考え方を説明しているのは教科書や資料集のため、数学が苦手な人ほど教科書に立ち返ることが大切です。ここで、大切なポイントがあります。それは文字の意味を理解することです。例えば、次の公式は数学I【図形と計量】で学習する、正弦定理という公式です。

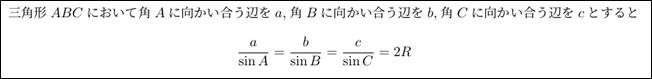
　さて、既習済みの人はこのRが何を表しているか分かりますか？正解は、三角形ABCにおける外接円の半径を表します。このRの意味が分からないと、実際の計算でもこの公式を使いこなすことができません。なので教科書からインプットする際は、文字の意味も理解しながら進めましょう。

演習ノートの書き方

　数学の演習ノートを作る際には、他の科目と異なりいくつかポイントがあります。

1.答えだけでなく、解答手順も書く
　数学は答えだけでなく、解答に至るプロセスを理解することも大切です。数学は記述式での出題も多いため流れをつかめるように、途中式などは省略せず書きましょう。

2.丸つけの時は、細かな部分までチェックする
　1に似ていますが、丸つけの際には答えが〇・×だけでなく、答えまでに書いた解答でおかしな部分がないかをチェックしてください。例えば、公式ミス、文字の書き間違い、条件不足等です。基準は模範解答を参照してください。基本的には模範解答は必要最低限のことが書かれているので、模範解答に書かれてあり、自分の解答に書かれていないものは書き足すようにしましょう。また、それらは全てノートに書き込みましょう。

3.基本的には問題は書かない、問題集のページ・問題番号は記載する
　やりがちな事ですが、問題を書き写すのは時間がもったいないので、問題集のページや問題番号を変わりに記入するようにしてください。作成例を載せておきます。ノートを分割し、左側で解答、右側でメモややり直しを記入します。参考にしてください。

演習ノートの作成例

暗記数学と思考数学を使い分ける

　ただ数学を学習するといっても、大きく2つのパターンに分けられます。それが「暗記数学」と「思考数学」というものです。詳しくみていきましょう。まず、「暗記数学」は名前の通り、覚えることが中心となります。何を覚えるのかというと、公式や定理は大前提なのですが、解答の定石や考え方を覚えることです。例えば、次のような問題を考えましょう。

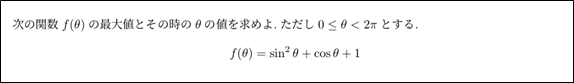
　これは数学Ⅱ【三角関数】での典型問題となります。この問題をみて、みなさんはどのようなアプローチをしますか？既習済みの人は一度考えてみましょう。

　この問題での解答例としては、三角関数の公式と変数変換を用いて二次関数に落とし込むのが定石となります。以下に模範解答を載せておきますので、参考にしてください。（まだ習っていない人は読み飛ばしていただいて大丈夫です。）言いたいことは、このような解答の手順が浮かぶのは経験があるからです。同じような問題を解いたことがある、知っていることで問題へのアプローチはいくつも考えることができるのです。つまり、様々な問題を繰り返し通して解法パターンを頭にインプットすることが問題を解けるかどうかにつながります。繰り返し学習することについては以降にも記載しておりますので、そちらも併せてご覧ください。

先の問題の解答例

　次に「思考数学」についてです。思考数学というよりも、数学的な思考力といった方がわかりやすいかもしれませんね。例えば、前提から結論への道筋を立てる「論理的思考力」、繰り返しや規則性を見つける「パターン認識力」、大きな問題を小さく分割して最終的に統合する「分解・統合力」などがあげられます。

　具体的な例で考えてみましょう。「論理的思考力」は分かりやすいと思いますが、答案の記述や証明問題です。友達との会話とは異なるので、正しい日本語使いや論理展開力が必要になります。「パターン認識力」は数学Aでの【確率】や数学BCの【数列】などがわかりやすいです。規則性を見出して、解答に結びつける力はこれらの分野で大きく活躍します。「分解・統合力」はテストや入試問題で必要となります。難しい問題を解く際にいきなり解答を求めようとするのではなく、解答のために必要な情報を細かく求める、それらの情報を合わせることで解答に結びつけることができるのです。

　このような力は一朝一夕で身につくものではなく、日々の演習によって培われる力となります。すぐに実感をすることはできませんが、諦めず根気よく努力をすることで確実に力をつけることができます。

「口頭再現」で定着度を高めるコツ

　数学の勉強には問題を見たら解き方がスラスラと言えるようになるための勉強法として「口頭再現法」という学習方法があります。この学習法では模範解答をもとに、問題を自分の言葉で口頭説明するように解法を記憶していきます。やることは単純です、理解できなかった問題、間違った問題を声に出して説明するように解答の流れを口に出して覚えます。

これを実施するにあたっていくつかポイントがあります。

1.最初は模範解答を見ながらでよい
　到達目標は正しい解答を何も見ずに言えることなので、分からないうちは解答をみて問題の流れ・パターンを暗記して、基本的な考え方を身につけましょう。

2.言葉だけでなく、紙を用いてよい
　問題形式によっては、言葉のみでは理解しづらい部分があるので、必要であれば紙とペンを用いて誰かに教えるように解答を説明しましょう。

3.覚えるではなく理解する
　口頭暗記といっても、その問題における知識は理解している前提になります。抜けがある公式や定理がある場合は、それらを理解したうえで実施しましょう。

4.計算は省略してよい
　目的は解答の流れがすぐに頭に浮かぶことです。複雑な計算等は省略するなり、解答をみるなりしてよいです。

5.目安は5回繰り返す
　解き方が3回連続でスラスラいえるようになるのが達成の目安です。そのためには最低5回繰り返すと達成できます。ただし、問題の難易度にもよるので10回程度までかかる問題もあります。

6.1日3問は新規の問題を取り入れる
　毎日理想は5問、最低でも3問は実施しましょう。毎日3問でも1ヶ月で約100問の暗記となります。

　

■効果倍増の復習法とスケジュール管理

　くり返しになりますが、数学は復習ややり直しがとても大切な科目です。ここでは、具体的な復習方法や復習スケジュールの作り方を紹介します。

1問1問しっかり理解するための復習サイクルと反復練習

　日々の問題演習で解いたけど、テストで解き方を忘れてしまった経験はありませんか？前述においても繰り返しが大切ということを書いていますが、1度の演習ではなかなか身につきません。エビングハウスの忘却曲線というものがあります。覚えた時点での記憶率を100%としたとき、その記憶保持率は1日で74%も失われます。

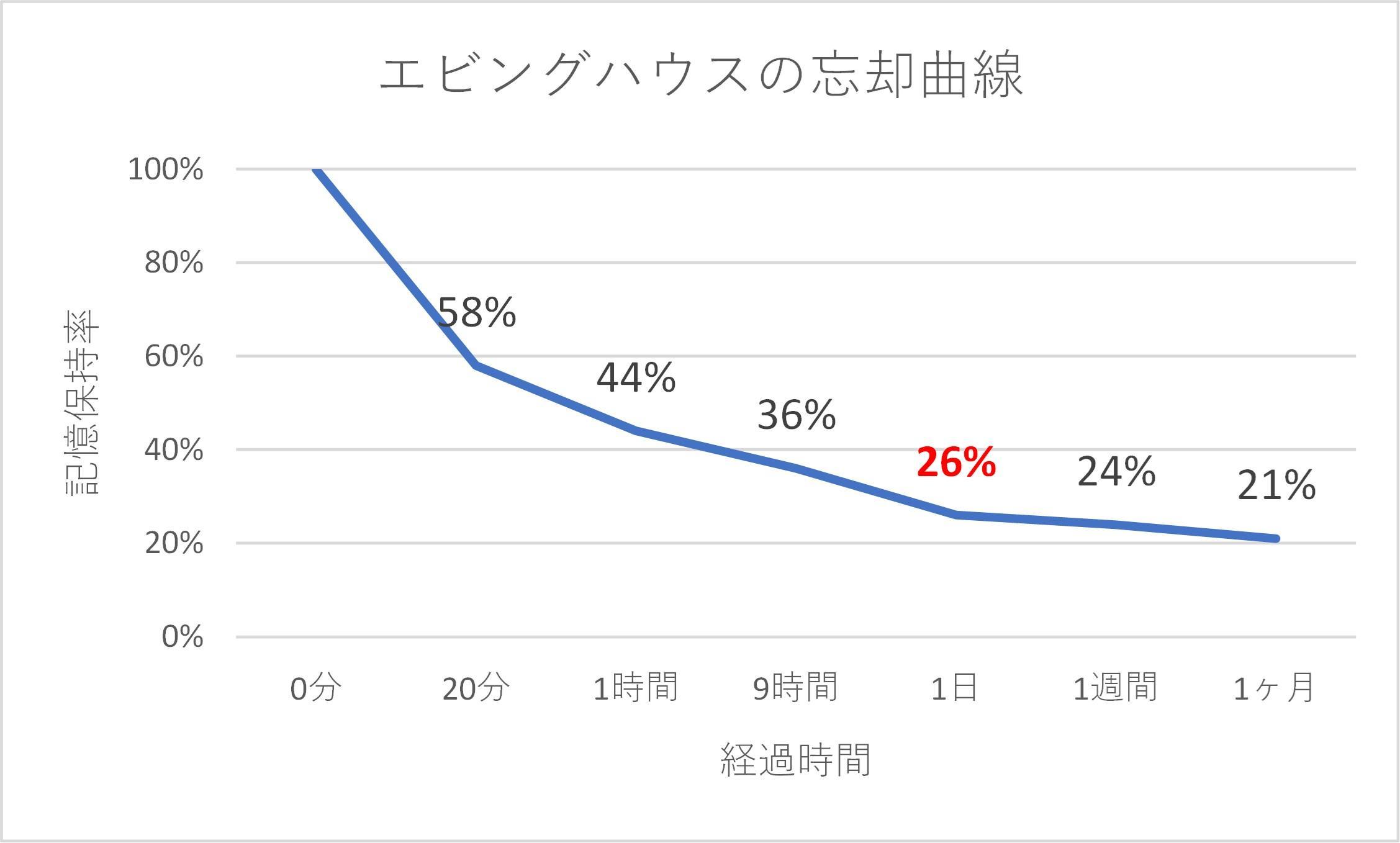
エビングハウスの忘却曲線

　つまり、その時に復習したとしても1日後にはほぼ忘れてしまうのです。これを踏まえて、具体的な復習サイクルとして次のようなものがおすすめです。

　復習の回数は4～5回程度実施するとよいです。具体的な復習タイミングは次の通りです。

1回目：復習当日

2回目：翌日 or 翌々日
　エビングハウスの忘却曲線によれば丁度、忘れかけのタイミングになります。

3回目：1週間後
　復習をしっかりしていると、1週間後の時点でもある程度思い出すことができます。ここで再度復習を行うことで、さらに定着します。

4回目：テスト前
　3回復習するとほとんど覚えてきます。テスト前に再度復習して本番に備えましょう。

5回目：テスト後
　本番で実力を出せたかを最後に復習をしましょう。忘れている部分があれば、最後にチェックしましょう。

苦手克服までのステップアッププラン

　苦手単元こそ復習を丁寧に実施する必要があります。苦手克服のため、復習ステップを細かくしてみると以下のようになります。

Step1.復習する問題を理解する

　数学の問題は公式や定理などの考え方を組み合わせて考えます。そのため各問題で必要な基礎知識や公式を再確認して、この問題はどのように解答にたどり着いているのか、何を求めているのか、問題ごとに理解しましょう。

Step.2解法の再現

　口頭再現のパートでも書きましたが、次のステップは模範解答をもとに解法の再現ができることです。前述の復習サイクルと合わせて、各復習でのタイミングで何も見ずに解答を再現できるレベルに仕上げましょう。

Step3. 応用問題を解いてみる

　解きなおしを実施した後に、初見問題として条件が異なる問題や類題問題に挑戦してみましょう。テストや入試などでの初見問題に対するアプローチ練習として実施します。ポイントとしては、解きなおしをした問題と同様に公式や考え方が使えないかを試してみることです。また復習の際に、解けていないのであればなぜ解けなかったのか、解きなおした問題とどこが違うのかを分析しましょう。

Step4. （受験生のみ）過去問や類似問題を解いてみる

　Step3のさらに応用編です。実際に受験する大学の過去問を解いてみましょう。自分の解きなおした問題での知識で戦えるのか、足りないものは何かを見つけましょう。

成績アップの鍵はケアレスミスの減少

　数学の問題を解くうえで、ケアレスミスはつきものです。しかし、そのケアレスミスをなくすことは成績アップに大いにつながります。ここでは、そんなケアレスミスとの付き合い方を紹介します。

　

■ケアレスミスへの心構えと改善策

　まずはケアレスミスの考え方になりますが、極端な話、本番（定期テストや受験）でしなければいいのです。落ち込むのではなく、本番で失敗しないように気をつけたり、改善策をとるのです。「次は間違えないから、OK」という心構えでは、同じような間違いを繰り返してしまいます。ケアレスミスをしたなら、どんな些細なものでもチェックしてください。そして、次は絶対に間違えないようにしましょう。具体的な改善策として、オススメなのは自分専用のケアレスミスノートを作りましょう。イメージは下図の通りです。

ケアレスミスノートの作成例

　このノートをテスト・模試・受験前に確認するだけで本番での意識ことは変わるはずです。自分はどんなケアレスミスをするのかわからない人はぜひ作ってみましょう。

　

■まとめ：高校数学は基礎と反復が最大のポイント

　いかがでしたでしょうか。数学は他の科目と比較しても苦手な学生は多いです。しかし、数学でつまずく人は基本的な部分の理解不足が多いです。正しい方法でインプットと復習をして、基礎から完璧にすることで苦手な分野の克服をすることができます。基本的なインプットが完了すれば、後は自分で使いこなせるようになるまで、演習と復習を繰り返すのみです。参考になったものがあれば、今日から実行してみましょう。皆さんの数学の認識が変わって、少しでも得意になっていただけると幸いです。最後までご覧いただきありがとうございました。

数学の学習鳥瞰図はコチラ▶学習鳥瞰図　数学.pdf

　

＜文／開成教育グループ　大学受験専門館　草津教室　奥田悠陽＞